Spectral Smoothing Unveils Phase Transitions in Hierarchical Variational Autoencoders

Abstract

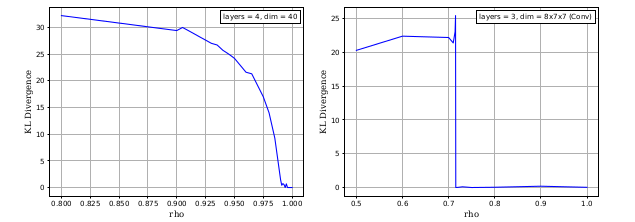
Variational autoencoders with deep stochastic hierarchies are known to suffer from the problem of posterior collapse, where the top layers fall back to the prior and become independent of input. We suggest that the hierarchical VAE objective explicitly includes the variance of the function parameterizing the mean and variance of the latent Gaussian distribution which itself is often a high variance function. Building on this we generalize VAE neural networks by incorporating a smoothing parameter motivated by Gaussian analysis to reduce higher frequency components and consequently the variance in parameterizing functions. We show this helps to solve the problem of posterior collapse. We further show that under such smoothing the VAE loss exhibits a phase transition, where the top layer KL divergence sharply drops to zero at a critical value of the smoothing parameter that is similar for the same model across datasets. We validate the phenomenon across model configurations and datasets.