Abstract
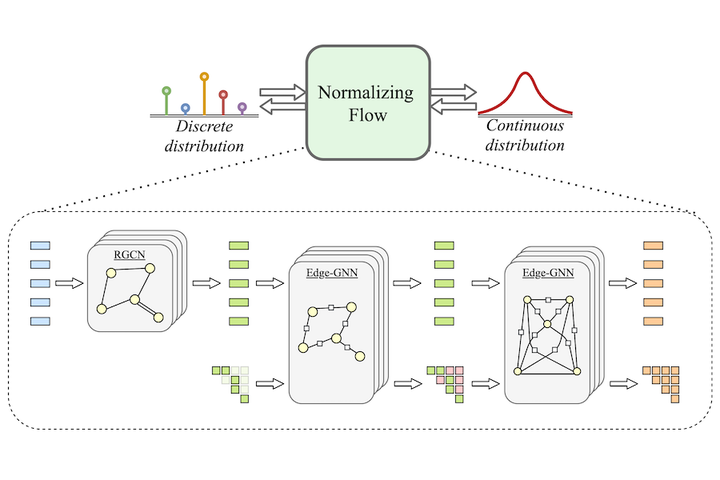
Despite their popularity, to date, the application of normalizing flows on categorical data stays limited. The current practice of using dequantization to map discrete data to a continuous space is inapplicable as categorical data has no intrinsic order. Instead, categorical data have complex and latent relations that must be inferred, like the synonymy between words. In this paper, we investigate Categorical Normalizing Flows, that is normalizing flows for categorical data. By casting the encoding of categorical data in continuous space as a variational inference problem, we jointly optimize the continuous representation and the model likelihood. Using a factorized decoder, we introduce an inductive bias to model any interactions in the normalizing flow. As a consequence, we do not only simplify the optimization compared to having a joint decoder, but also make it possible to scale up to a large number of categories that is currently impossible with discrete normalizing flows. Based on Categorical Normalizing Flows, we propose GraphCNF a permutation-invariant generative model on graphs. GraphCNF implements a three step approach modeling the nodes, edges, and adjacency matrix stepwise to increase efficiency. On molecule generation, GraphCNF outperforms both one-shot and autoregressive flow-based state-of-the-art.