Differentiable Mathematical Programming for Object-Centric Representation Learning

Abstract

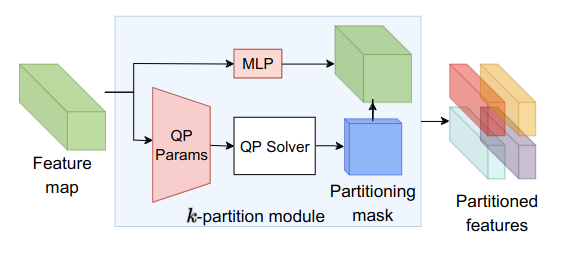
We propose topology-aware feature partitioning into $k$ disjoint partitions for given scene features as a method for object-centric representation learning. To this end, we propose to use minimum $s$-$t$ graph cuts as a partitioning method which is represented as a linear program. The method is topologically aware since it explicitly encodes neighborhood relationships in the image graph. To solve the graph cuts our solution relies on an efficient, scalable, and differentiable quadratic programming approximation. Optimizations specific to cut problems allow us to solve the quadratic programs and compute their gradients significantly more efficiently compared with the general quadratic programming approach. Our results show that our approach is scalable and outperforms existing methods on object discovery tasks with textured scenes and objects.