Scalable Subset Sampling with Neural Conditional Poisson Networks

Abstract

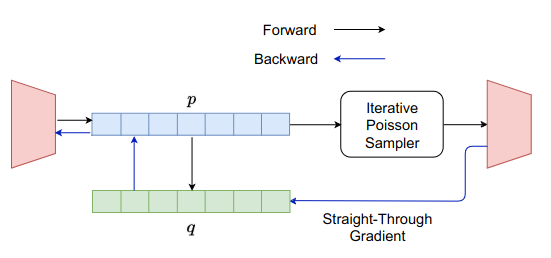
A number of problems in learning can be formulated in terms of the basic primitive of sampling $k$ elements out of a universe of $n$ elements. This subset sampling operation cannot directly be included in differentiable models, and approximations are essential. Current approaches take an order sampling approach to sampling subsets and depend on differentiable approximations of the Top-$k$ operator for selecting the largest $k$ elements from a set. We present a simple alternative method for sampling subsets based on conditional Poisson sampling. Unlike order sampling approaches, the complexity of the proposed method is independent of the subset size, which makes the method scalable to large subset sizes. We adapt the procedure to make it efficient and amenable to discrete gradient approximations for use in differentiable models. Furthermore, the method allows the subset size parameter $k$ to be differentiable. We validate our approach extensively, on image and text model explanation, image subsampling and stochastic $k$-nearest neighbor tasks outperforming existing methods in accuracy, efficiency and scalability.