Low Bias Low Variance Gradient Estimates for Boolean Stochastic Networks

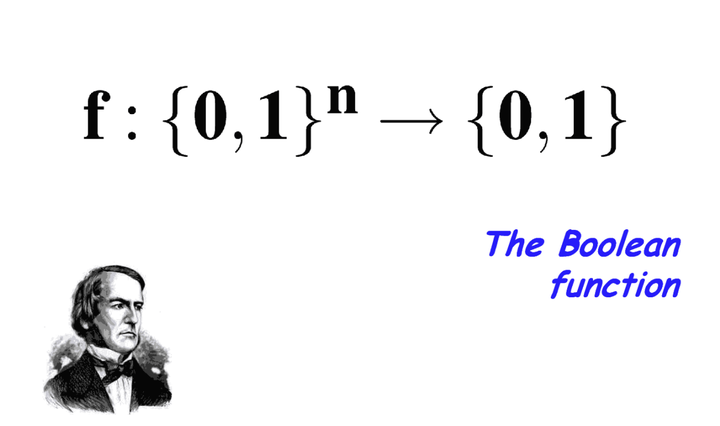
Abstract

Stochastic neural networks with discrete random variables are an important class of models for their expressiveness and interpretability. Since direct differentiation and backpropagation is not possible, Monte Carlo gradient estimation techniques are a popular alternative. Efficient stochastic gradient estimators, such Straight-Through and Gumbel-Softmax, work well for shallow stochastic models. Their performance, however, suffers with hierarchical, more complex models. We focus on stochastic networks with Boolean latent variables. To analyze such networks, we introduce the framework of harmonic analysis for Boolean functions to derive an analytic formulation for the bias and variance in the Straight-Through estimator. Exploiting these formulations, we propose\emph {FouST}, a low-bias and low-variance gradient estimation algorithm that is just as efficient. Extensive experiments show that FouST performs favorably compared to state-of-the-art biased estimators and is much faster than unbiased ones.