Hyperbolic Graph Codebooks
Abstract
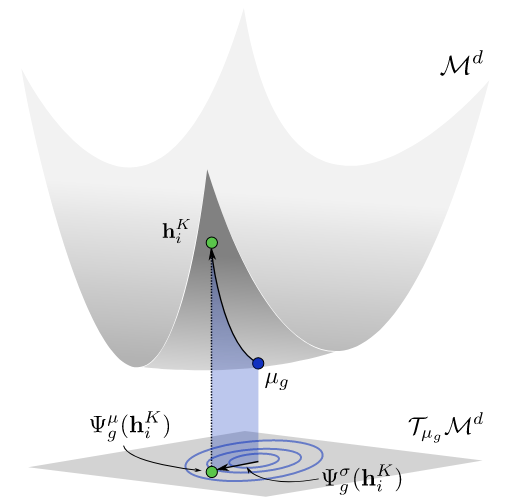
This work proposes codebook encodings for graph networks that operate on hyperbolic manifolds. Where graph networks commonly learn node representations in Euclidean space, recent work has provided a generalization to Riemannian manifolds, with a particular focus on the hyperbolic space. Expressive node representations are obtained by repeatedly performing a logarithmic map, followed by message passing in the tangent space and an exponential map back to the manifold at hand. Where current hyperbolic graph approaches predominantly focus on node representation, we propose a way to aggregate over nodes for graph-level inference. We introduce Hyperbolic Graph Codebooks, a family of graph encodings where a shared codebook is learned and used to aggregate over nodes. The resulting representations are permutation invariant and fixed-size, yet expressive. We show how to obtain zeroth-order codebook encodings through soft assignments over hyperbolic distances, first-order encodings with anchored logarithmic mappings, and second-order encodings by computing variance information in the tangent space. Empirically, we highlight the effectiveness of our approach, especially when few examples and embedding dimensions are available.