Abstract
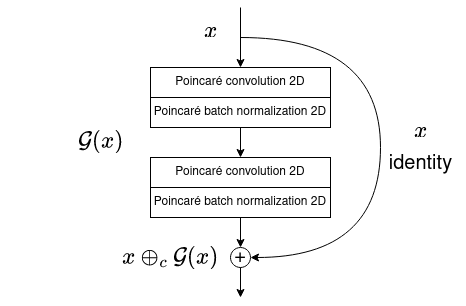
This paper introduces an end-to-end residual network that operates entirely on the Poincaré ball model of hyperbolic space. Hyperbolic learning has recently shown great potential for visual understanding, but is currently only performed in the penultimate layer(s) of deep networks. All visual representations are still learned through standard Euclidean networks. In this paper we investigate how to learn hyperbolic representations of visual data directly from the pixel-level. We propose Poincaré ResNet, a hyperbolic counterpart of the celebrated residual network, starting from Poincaré 2D convolutions up to Poincaré residual connections. We identify three roadblocks for training convolutional networks entirely in hyperbolic space and propose a solution for each: (i) Current hyperbolic network initializations collapse to the origin, limiting their applicability in deeper networks. We provide an identity-based initialization that preserves norms over many layers. (ii) Residual networks rely heavily on batch normalization, which comes with expensive Fréchet mean calculations in hyperbolic space. We introduce Poincaré midpoint batch normalization as a faster and equally effective alternative. (iii) Due to the many intermediate operations in Poincaré layers, the computation graphs of deep learning libraries blow up, limiting our ability to train on deep hyperbolic networks. We provide manual backward derivations of core hyperbolic operations to maintain manageable computation graphs.