Quasibinary Classifier for Images with Zero and Multiple Labels

Abstract

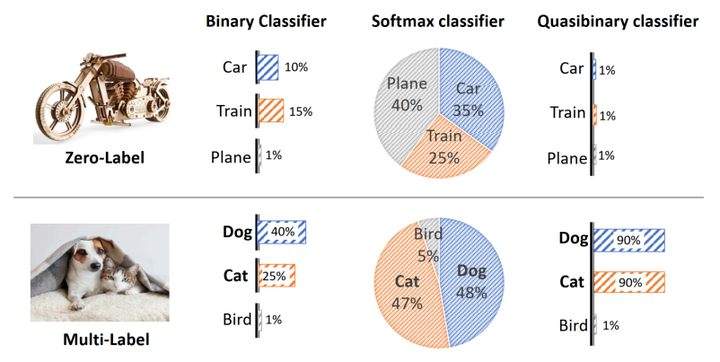
The softmax and binary classifier are commonly preferred for image classification applications. However, as softmax is specifically designed for categorical classification, it assumes each image has just one class label. This limits its applicability for problems where the number of labels does not equal one, most notably zero-and multi-label problems. In these challenging settings, binary classifiers are, in theory, better suited. However, as they ignore the correlation between classes, they are not as accurate and scalable in practice. In this paper, we start from the observation that the only difference between binary and softmax classifiers is their normalization function. Specifically, while the binary classifier self-normalizes its score, the softmax classifier combines the scores from all classes before normalisation. On the basis of this observation we introduce a normalization function that is learnable, constant, and shared between classes and data points. By doing so, we arrive at a new type of binary classifier that we coin quasibinary classifier. We show in a variety of image classification settings, and on several datasets, that quasibinary classifiers are considerably better in classification settings where regular binary and softmax classifiers suffer, including zerolabel and multi-label classification. What is more, we show that quasibinary classifiers yield well-calibrated probabilities allowing for direct and reliable comparisons, not only between classes but also between data points.