Abstract
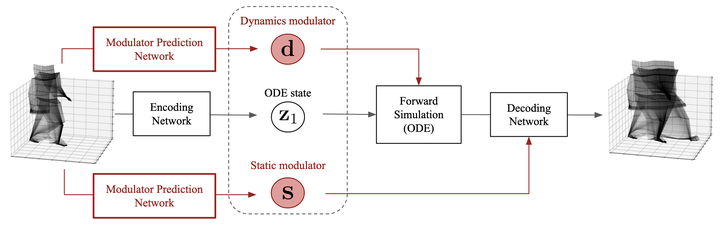
Neural ordinary differential equations (NODEs) have been proven useful for learning non-linear dynamics of arbitrary trajectories. However, current NODE methods capture variations across trajectories only via the initial state value or by auto-regressive encoder updates. In this work, we introduce Modulated Neural ODEs (MoNODEs), a novel framework that sets apart dynamics states from underlying static factors of variation and improves the existing NODE methods. In particular, we introduce time-invariant modulator variables that are learned from the data. We incorporate our proposed framework into four existing NODE variants. We test MoNODE on oscillating systems, videos and human walking trajectories, where each trajectory has trajectory-specific modulation. Our framework consistently improves the existing model ability to generalize to new dynamic parameterizations and to perform far-horizon forecasting. In addition, we verify that the proposed modulator variables are informative of the true unknown factors of variation as measured by R^2 scores.