Ai-Sampler: Adversarial Learning of Markov Kernels with Involjtive Maps

Abstract

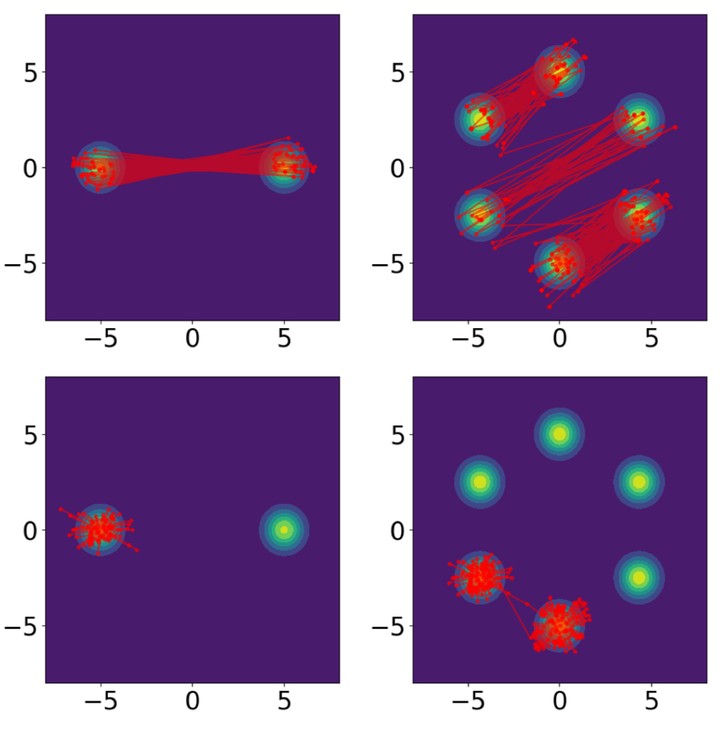
Markov chain Monte Carlo methods have become popular in statistics as versatile techniques to sample from complicated probability distributions. In this work, we propose a method to parameterize and train transition kernels of Markov chains to achieve efficient sampling and good mixing. This training procedure minimizes the total variation distance between the stationary distribution of the chain and the empirical distribution of the data. Our approach leverages involutive Metropolis-Hastings kernels constructed from reversible neural networks that ensure detailed balance by construction. We find that reversibility also implies C2-equivariance of the discriminator function which can be used to restrict its function space.