 | Convex Reduction of High-Dimensional Kernels for Visual Classification In IEEE Conference on Computer Vision and Pattern Recognition 2012. [bibtex] [pdf] [url] |
Abstract
Limiting factors of fast and effective classifiers for large
sets of images are their dependence on the number of images
analyzed and the dimensionality of the image representation. Considering the growing number of images as a given, we aim to reduce the image feature dimensionality in this paper. We propose reduced linear kernels that use only a portion of the dimensions to reconstruct a linear kernel. We formulate the search for these dimensions as a convex optimization problem, which can be solved efficiently. Different from existing kernel reduction methods, our reduced kernels are faster and maintain the accuracy benefits from non-linear embedding methods that mimic non-linear SVMs. We show these properties on both the Scenes and PASCAL VOC 2007 datasets. In addition, we demonstrate how our reduced kernels allow to compress Fisher vector for use with non-linear embeddings, leading to high accuracy.
What is more, without using any labeled examples the
selected and weighed kernel dimensions appear to correspond
to visually meaningful patches in the images.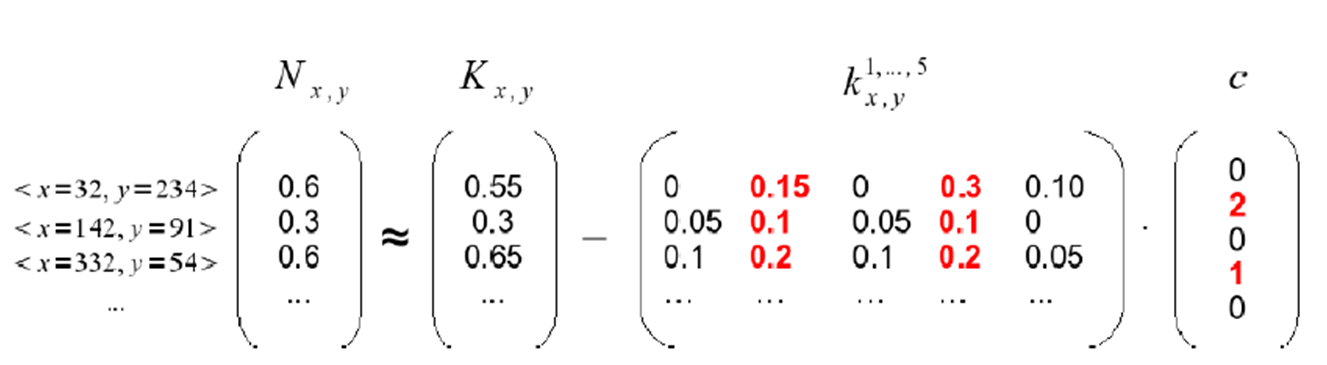
Bibtex Entry
@InProceedings{GavvesCVPR2012,
author = "Gavves, E. and Snoek, C. G. M. and Smeulders, A. W. M.",
title = "Convex Reduction of High-Dimensional Kernels for Visual Classification",
booktitle = "IEEE Conference on Computer Vision and Pattern Recognition",
year = "2012",
url = "https://ivi.fnwi.uva.nl/isis/publications/2012/GavvesCVPR2012",
pdf = "https://ivi.fnwi.uva.nl/isis/publications/2012/GavvesCVPR2012/GavvesCVPR2012.pdf",
has_image = 1
}